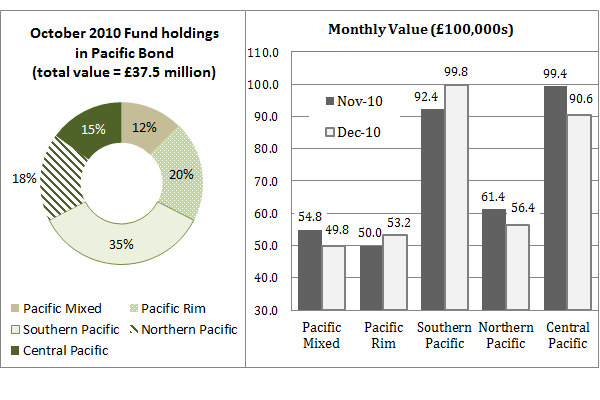
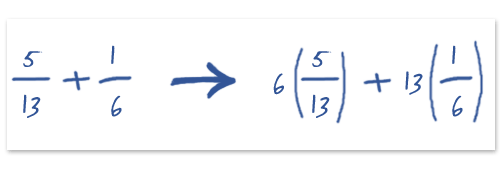Employers use numerical reasoning tests to help them predict who has the required numerical abiltiy to perform well in the job, so naturally they have to have a point at which they say ‘yes you’re in’ or ‘no, sorry’. In real life, most employers are not this black and white when it comes to your numerical test score; they will look at everyone’s score and compare them against a set of other competencies and success factors. So for example if you scored highly in a partner interview and you have relevant work experience, but were not the highest performer in your numerical test, the recruiting organisation may well decide that you are sill the best person for the job. It’s all relative, as they say.

Very large organisations (such as large professional services firms or firms with large graduate schemes) cannot afford to study each separate applicant in this pragmatic way. Instead they may use an online numerical test as an online sifting tool. The computer will automatically highlight candidates achieving a certain score and put them forward to the next stage of the selection process. If you don’t make this automatic cut, you will be rejected by that company. Often in this situation the company says that you are not allowed to re-apply for another minimum period of time, usually 12 months.

If you don’t make the cut, the truth is that you would probably have found the job frustrating, demoralising  or stressful. The whole point in psychometric testing is that it is the best tool we have for predicting who will be suited to the role. Psychometric testing (including numerical tests) are based on years of research and development. So if the test says you are not suitable, the chances are the test is right and you should be please that you did not get put in a job for which you were not suitable.

When you are preparing for your numerical reasoning test, you should think carefully about where and when you practice. The best environment for practising, it goes without saying, is one which is quiet, comfortable and familiar.

In addition you should consider the following:

Interruptions: put a sign on your door to let your housemates know that you are not to be disturbed.
Same desk: if your real test is online, and therefore can be taken wherever you like, try to make it the same place as where you have practised (e.g. your room or study). This repetition and familiarity will help replicate your performance.
Noise or disturbances: pay attention to your surroundings; is there an annoying draft, humming, or do you have a wobbly desk?

Should you get your clever friend to help with your online (unsupervised) test? Or rather, if you do, will anyone find out?!

This is one of the more common questions I get asked by candidates, because they want to know how easy it would be to cheat.

The short answer is: no; you should not get anyone else to help you with your online test and yes, they probably will find out.

The longer answer, and the reason why, is that modern numerical test technology detects subtle pattern behavior in the way you respond to each question. Some companies then ask candidate to take a follow-up test at their offices. If the ‘fingerprints’ of your test-taking style don’t match, they can ask some pertinent questions about why the results differ.

Another reason not to cheat is that the tests are there to assess whether you will be a good fit for the role. If don’t have the numerical ability to perform, you will spend the rest of your career being passed over for promotion, struggling, and more likely to leave. So whilst this doesn’t sound a valid reason whilst you’re unemployed, the truth is that you will being selected for a job to which you are not suited.

Another frequently-asked question by candidates is what is the pass mark? How many questions should they be aiming to get right?

The answer to this depends on knowing what a percentile score is. Because employers will have a ‘select in / sift out’ percentile score in mind when deciding the cut-off percentile score. The cut-off percentile score can be whatever the employer decides they are looking for, but typically speaking companies such as the big graduate recruiters will use the 40th-50th percentile as a benchmark. Some elite institutions may go as far as stipulating the 90th percentile (i.e. they will take only the top 10%), but this is rare.

What is a percentile? It is the percent of the comparison group who have a score lower than yours. So for example, scoring in the 4oth percentile means that 40% of the comparison group (referred to as the norm group) had a score below yours, and 60% had a score higher than yours.

The norm group is a group of people who have taken the test before, against whom your score is compared. Test publishers will have many different norm groups depending on what the employer wants to benchmark you against. So there are graduate norm groups, senior manager norm groups, international administrative workers norm groups, bespoke norm groups for a specific company, and even a specific role…just about any group of test takers can generate score data against which your score can be comaped.

The reason percentile scores and norm groups are used is that this is the best way to make comparisons. If you score 19/24, is that good? Average? Who knows, until you know what other people got. It may be that the test was really easy and that the average score from other participants is 22/24. The only way to capture your relative performance is to use percentile scoring against a norm group, which is what employers do.

You can read more about percentile scores in our page here: percentiles.

If it can be proved that you cheated in any of your tests, you will be ejected from the selection process. This is because almost certainly you will have agreed to the conditions attached to taking a numerical test for selection, which will have contained a declaration that you have attempted the test on your own without help, without distorting the results  without deceitful intentions etc. And in the unlikely event that you didn’t have to agree to such terms, let’s face it; very few companies would want to  employ a conniving candidate.

So, how do they detect cheating? Various means. Test publishers spend multiple thousands of pounds and many man-hours ensuring their tests are cheat-proof. The most common practice is to give (or pose the prospect of) a re-test under supervised conditions. So if you get a friend to help, or you employ some other deceitful means to distort your score on your online (unsupervised) test, you will probably be found out when you take a re-test in the employer’s office where you are unable to employ such tactics. At this point, if there are significant variations between your supervised and unsupervised test scores, serious suspicions of misconduct will arise.

So don’t cheat!

Almost always yes. The reason for this is that most numerical reasoning tests used in employment selection are trying to measure your numerical ability in a work setting, where there is usually a calculator available. Very few roles nowadays require employees to perform complex mental calculations, so as such very few selection tests assess this ability. If you are given a test where calculators are not permitted, you will be supervised (which is more expensive than an online unsupervised test for the employer) and the maths involved will be more straightforward.

Given that calculators are almost always permitted, what one do you choose to use? If you get the choice (for example you are taking the test remotely from home) try to use a calculator with which you are familiar. Knowing instinctively where the buttons are and how it works will save  a few vital seconds during your test. Also try to use one which displays your keystrokes on the screen (all scientific calculators do this) because this will help you see where you got to in a  calculation involving several input steps. We’ve all had the feeling whilst inputting numbers to a calculator that we’ve miss-keyed something, or forgotten where we got to, so being able to see this on-screen is a big help.